DataLab

2018-04-18

南京航空航天大学计算机组成原理实验 Lab1 Data-Lab

bitXor

Discription

x^y using only ~ and &

Legal ops

& ~

Max ops

Code

1
2
3

int bitXor(int x, int y) {
    return ~((~(~x&y))&(~(x&~y)));
}

Thought

用数字电路的思想，x xor y = (not x and y) or (x and not y)，然后转化为代码即可。

minusOne

Discription

return a value of -1

Legal ops

! ~ & ^ | + << >>

Max ops

Code

1
2
3

int minusOne(void) {
    return ~0;
}

Thought

-1的补码为0xFFFFFFFF，恰好是0按位取反的结果。

leastBitPos

Description

return a mask that marks the position of the least significant 1 bit.

If x == 0, return 0

Legal ops

! ~ & ^ | + << >>

Max ops

Code

1
2
3

int leastBitPos(int x) {
    return (~x+1)&x;
}

Thought

首先要理解题意，least significant 1 bit是指最低有效为1的位，也就是求最低有效为1的位的位置的掩码。其实本质上就是找到最后一个1，然后前面全变成0。最终效果是除了LS1B为1，其他位全为0。

假设从第一位开始，第i位为LS1B。那么1~i-1位为0，i位为1。首先x按位取反，那么1~i-1位均为1，第i位为0，>i的位均取反。然后+1，加一后，1~i-1位均为0，i位为1，其余位取反。那么相与之后即得到答案。

allEvenBits

Description

return 1 if all even-numbered bits in word set to 1

Examples

allEvenBits(0xFFFFFFFE) = 0

allEvenBits(0x55555555) = 1

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int allEvenBits(int x) {
    x = x & (x >> 16);
    x = x & (x >> 8);
    x = x & (x >> 4);
    x = x & (x >> 2);
    return (x & 0x01);
}

Thought

这个题的难点在于对操作数的要求，要限制在12次操作以内。很朴素的思想就是把所有偶数位都提取出来，可以定义一个数，每次都与该中间变量相与。

无疑这样的复杂度有些高，所以要想其他的办法。我们观察到我们只需要知道是否偶数位全为1即可，假如某一个偶数位为0，它相与之后必定答案为0。所以我们想到，可以用移位操作，每次对半切这个01串，让对应位相与，这样偶数位与偶数位与，奇数位与奇数位与，最终看最低位为0还是1即可。

byteSwap

Description

swaps the n-th byte and the m-th byte

You may assume that 0 <= n <= 3, 0 <= m <= 3

Examples

byteSwap(0x12345678, 1, 3) = 0x56341278

byteSwap(0xDEADBEEF, 0, 2) = 0xDEEFBEAD

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int byteSwap(int x, int n, int m) {
    int t1 = (x >> (n << 3)) & 0xFF;
    int t2 = (x >> (m << 3)) & 0xFF;
    x = (x & (~ (0xFF << (m << 3)))) | (t1 << (m << 3));
    x = (x & (~ (0xFF << (n << 3)))) | (t2 << (n << 3));
    return x;
}

Thought

第一思路是联想到用三次异或实现两个数值交换，只是在这里不是两个数值，而是一个数值里的两个Byte。

于是我做了一个大胆的假设：n<m。

第一版代码：

int byteSwap(int x, int n, int m) {
    int c=m+(~n+1);
    x = x ^ ((x << (c << 2)) & (0xFF << (m << 2)));
    x = x ^ ((x >> (c << 2)) & (0xFF << (n << 2)));
    x = x ^ ((x << (c << 2)) & (0xFF << (m << 2)));
    return x;
}

然而第一组数据是 0x80000000 1 0，输入的n>m……

然后仍然不死心，那就把c取个绝对值吧！怎么用位运算取绝对值呢……

当是正数时，应该数值不变，当是负数时，取反加一。

但是不能使用分支语句。

于是用扩展的符号位。

int byteSwap(int x, int n, int m) {
    int c=m+(~n+1);
    int cc = c >> 31;
    c = (c ^ cc) - cc;
    x = x ^ ((x << (c << 3)) & (0xFF << (m << 3)));
    x = x ^ ((x >> (c << 3)) & (0xFF << (n << 3)));
    x = x ^ ((x << (c << 3)) & (0xFF << (m << 3)));
    return x;
}

如果是正数，那扩展符号位为0，那么一个数异或0不变，再减0还是不变的。

如果是负数，那么扩展符号位为0xFFFFFFFF，那么按位异或1就是每一位取反，然后再-(-1)就是+1。

结果还是错误的……

算了还是用最基础的办法吧。开两个临时变量t1,t2存储第n个字节和第m个字节的值，然后把x上的m，n两个字节的值弄成0，再或一下就进去了。

isAsciiDigit

Description

return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters ‘0’ to ‘9’)

Examples

isAsciiDigit(0x35) = 1.

isAsciiDigit(0x3a) = 0.

isAsciiDigit(0x05) = 0.

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int isAsciiDigit(int x) {
    int t1 = (x + (~0x30 + 1)) >> 31;
    int t2 = (0x39 + (~x + 1)) >> 31;
    return (t1 | t2) + 1;
}

Thought

首先直观的想到，如果可以用减法和分支语句，那么只要判断一下(0x30 - x <= 0 && x - 0x39 <=0)即可。首先说，减法可以用加补码实现。那么做减法后，与0比较其实就是比较符号位，若符号位为1，则说明小于0，若为0，则说明大于0。那么我们可以扩展符号位，用算术右移31位，如果符号位为1，那么答案为0xFFFFFFFF，如果符号位为0，那么答案为0x00000000。

那么确定最终返回0还是1，我们观察两个减法右移31位以后的结果t1和t2，两个分别都最多有两种可能。那么总体最多有四种可能。

1°当t1=0xFFFFFFFF, t2=0xFFFFFFFF，说明x\<0x30 && 0x39\<x，显然不可能出现。

2°当t1=0xFFFFFFFF, t2=0x00000000，说明x\<0x30 &&="" 0x39\="">x，这是不满足题意得，应该返回0。而t1 | t2 = 0xFFFFFFFF，那么+1后就成了0x00000000。

3°当t1=0x00000000, t2=0xFFFFFFFF，说明x > 0x30 && 0x39 \< x，这也是不满足题意得，应该返回0。而t1 | t2 = 0xFFFFFFFF，那么+1后也成了0x00000000。

4°当t1=0x00000000, t2=0x00000000，说明x > 0x30 && 0x39 > x，满足题意，返回1。而t1 | t2 = 0x00000000，那么+1后为1。

所以我们观察到一个规律，(t1|t2)+1就是答案。

satMul2

Description

multiplies by 2, saturating to Tmin or Tmax if overflow

Examples

satMul2(0x30000000) = 0x60000000

satMul2(0x40000000) = 0x7FFFFFFF (saturate to TMax)

satMul2(0x60000000) = 0x80000000 (saturate to TMin)

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int satMul2(int x) {
  int xx = x << 1;
  return (xx & (~((x >> 31) ^ (xx >> 31)))) + ((((x >> 31) ^ (xx >> 31)) << 31) ^ ((~(x >> 31)) & ((x >> 31) ^ (xx >> 31))));
}

Thought

首先肯定要判溢出。带符号数判溢出是用x的符号位和2*x的符号位比较，相同没溢出，不同溢出，所以做异或的话，结果0不溢出，1溢出。

有四种情况，分别讨论。当不溢出时直接输出答案，正溢出时输出Tmax=0x7FFFFFFF，负溢出时输出Tmin=0x80000000。

观察到0x7FFFFFFFF = ~(0x80000000)，而0x80000000可以通过1<<31得到。

当溢出时，答案与x<<1无关，而x<<1的结果是不确定的，不方便处理，所以想到和~t相与，这样如果不溢出，t=0x00000000，~t=0xFFFFFFFF，x<<1不会变；而溢出的话，t=0xFFFFFFFF，~t=0x00000000，x<<1会变成0x00000000，方便处理。

当把x<<1的影响去除后，我们需要通过t1,t2,t来构造Tmax和Tmin。因为这一项只有当溢出的时候才起作用，所以0x80000000可以由t<<31得到。这样当不溢出的时候得到的就是0。

正溢出时，即t1=0x00000000,t=0xFFFFFFFF时输出~(t<<31)；负溢出时，即t1=0xFFFFFFFF,t=0xFFFFFFFF时输出t<<31；当正数不溢出时，即t1=0x00000000,t=0x00000000时输出0；当负数不溢出时，即t1=0xFFFFFFFF,t=0x00000000时输出0。列真值表：

t1\t	0	1
0	0	1
1	0	0

可以得到表达式为((t << 31) ^ ((~t1) & t))

int satMul2(int x) {
  int t1 = x >> 31;
  x = x << 1;
  int t2 = x >> 31;
  int t = t1 ^ t2;
  return (x & (~t)) + ((t << 31) ^ ((~t1) & t));
}

不知道这一份美丽的代码为什么报错说t未定义。和正确代码思路是一样的，只是正确的丑了一些。

subOK

Description

Determine if can compute x-y without overflow

Examples

subOK(0x80000000,0x80000000) = 1,

subOK(0x80000000,0x70000000) = 0,

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int subOK(int x,int y) {
    int t1 = x >> 31;
    int t2 = y >> 31;
    int t = t1 ^ t2;
    int cf = (x + (~y + 1)) >> 31;
    return (t & (t1 ^ cf)) + 1;
}

Thought

正-正和负-负不会溢出，只有正-负和负-正会溢出。

溢出的判断依据是：

x，y的符号位不同且相减后的符号位与x的符号位不同。

isLess

Description

if x < y then return 1, else return 0

Examples

isLess(4,5) = 1

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int isLess(int x, int y) {
    int t1 = x >> 31;
    int t2 = y >> 31;
    int t = (x + (~y + 1)) >> 31;
    return (~(~(t1 ^ t2) & t) + 1) | (~(t1 & ~t2) + 1);
}

Thought

错误思路：直接用x-y然后判断结果的符号位。

错误原因：有可能会溢出。

正确思路：先判断x，y的符号位，相同可以相减判断结果符号位，否则的话直接判断即可。列真值表很方便。

bitMask

Description

Generate a mask consisting of all 1’s lowbit and highbit

Examples

bitMask(5,3) = 0x38

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int bitMask(int highbit, int lowbit) {
    int x = ~0;
    x = x & (~0 << lowbit);
    x = x & ~((~0 << highbit) << 1);
    return x;
}

Thought

该题的意思是求一个掩码，这个掩码的highbit和lowbit之间全为1，其他全为0。那么初始值设为0xFFFFFFFF，然后把后lowbit位通过与操作置为0，同理将前面的也置为0。

leftBitCount

Description

returns count of number of consective 1’s in left-hand (most significant) end of word.

Examples

leftBitCount(-1) = 32, leftBitCount(0xFFF0F0F0) = 12

Legal ops

! ~ & ^ | + << >>

Max ops

Code

int leftBitCount(int x) {
  int t = x;
  int ans = 0;
  int tans = 0;
  
  tans = !(~(t >> 16)) << 4;
  ans = ans + tans;
  t = t << tans;

  tans = !(~(t >> 24)) << 3;
  ans = ans + tans;
  t = t << tans;

  tans = !(~(t >> 28)) << 2;
  ans = ans + tans;
  t = t << tans;

  tans = !(~(t >> 30)) << 1;
  ans = ans + tans;
  t = t << tans;
  
  tans = !(~(t >> 31));
  ans = ans + tans;
  t = t << tans;

  ans = ans + (~(t >> 31) + 1); 
  
  return ans;
}

Thought

32位，如果一位一位的处理，对每一位的处理需要两次计算，那么就64次计算。而最大50次计算，很容易想到用二分的思想。然而细节上不容易想到。

首先将高位移动到低位运算，第一次处理高16位。如果高16位为0xFFFF，那么按位取反后为0x0000，再取逻辑非为1。如果高16位不为0xFFFF，那么无论等于多少，运算结果均为0。假如前16位均为1，那么首先要先累加到答案上，然后舍弃掉高16位即可。如果前16位不全为1，那么应该不变。

后面的以此类推，可以总结，该方法的精妙之处在于，实际上实现了选择的功能。每次左移的位数是有规律可循的，如果前n位均为1，那么可以左移n位。n是2的倍数。否则不移动。不移动的话，处理的就是高位的一半，移动的话，处理的就是低位的一半，选择就体现在这里。

logicalNeg

Description

implement the ! operator, using all of the legal operators except !

Examples

logicalNeg(3) = 0, logicalNeg(0) = 1

Legal ops

~ & ^ | + << >>

Max ops

Code

1
2

Thought

同样用到二分的思路，每次对半切，只保留前半有效位，进行或运算，这样若x=0，则最终符号位为0，否则为1。再扩展符号位即可。

float_abs

Description

Return bit-level equivalent of absolute value of f for floating point argument f.

Legal ops

Any integer/unsigned operations incl. ||, &&. also if, while

Max ops

Code

unsigned float_abs(unsigned uf) {
    int iuf=uf;
    int n=~(0x80<<16)+1;
    if (iuf <= n) uf = uf ^ (1<<31);
    return uf;
}

Thought

首先我们写一个简单的C程序来看一下在整个32位的区域内，float的分布。

代码

#include<cstdio>
#include<iostream>
using namespace std;
bool all1(unsigned x,int high,int low)
{
    int flag = 1;
    for (int i=low;i<=high;i++)
        flag = flag & ((x >> i) & 1);
    if (flag) return true;
    return false;
}
bool all0(unsigned x,int high,int low)
{
    int flag=0;
    for (int i=low;i<=high;i++)
        flag = flag | ((x >> i) & 1);
    if (flag) return false;
    return true;
}
char arr[10][20] = {"po0","ne0","nefeiguigehuashu","poinfi","neinfi","poNaN","neNaN","neguigehuashu","poguigehuashu","pofeiguigehuashu"};
bool f[10];
void print(int i,int x)
{
    if (!f[x])
    {
        printf("0x%x %s\n",i,arr[x]);
        f[x]=true;
    }
}
int sign(int i)
{
    return (i>>31) & 1;
}
int main()
{
    int i=0x80000000;
//  printf("%d %d\n",sizeof(int),sizeof(float));
    for (;i<0x7FFFFFFF;i++)
    {
        if (i == 0x80000000) {print(i,1); continue;}
        if (i == 0x00000000) {print(i,0); continue;}
        if ((sign(i) == 1) && (all1(i,30,23)) && (all0(i,22,0))) {print(i,4); continue;}
        if ((sign(i) == 0) && (all1(i,30,23)) && (all0(i,22,0))) {print(i,3); continue;}
        if (all1(i,30,23) && (!all1(i,22,0) && !all0(i,22,0)))
        {
            if (sign(i) == 1)
            {
                print(i,6);
            }
            if (sign(i) == 0)
            {
                print(i,5);
            }
            continue;
        }
        if (all0(i,30,23) && !all0(i,22,0))
        {
            if (sign(i) == 1) print(i,2);
            if (sign(i) == 0) print(i,9);
            continue;
        }
        if (sign(i) == 1) print(i,7);
        if (sign(i) == 0) print(i,8);
    }

    i=0x7FFFFFFF;
    if (i == 0x80000000)
        {print(i,1);}
    else
    if (i == 0x00000000) {print(i,0);}
    else
    if ((sign(i) == 1) && (all1(i,30,23)) && (all0(i,22,0))) {print(i,4);}
    else
    if ((sign(i) == 0) && (all1(i,30,23)) && (all0(i,22,0))) {print(i,3);}
    else
    if (all1(i,30,23) && (!all1(i,22,0) && !all0(i,22,0)))
    {
        if (sign(i) == 1)
        {
            print(i,6);
        }
        if (sign(i) == 0)
        {
            print(i,5);
        }
    }
    else
    if (all0(i,30,23) && !all0(i,22,0))
    {
        if (sign(i) == 1) print(i,2);
        if (sign(i) == 0) print(i,9);
    }
    else
        if (sign(i) == 1) print(i,7);
    else
        if (sign(i) == 0) print(i,8);
    return 0;
}

输出

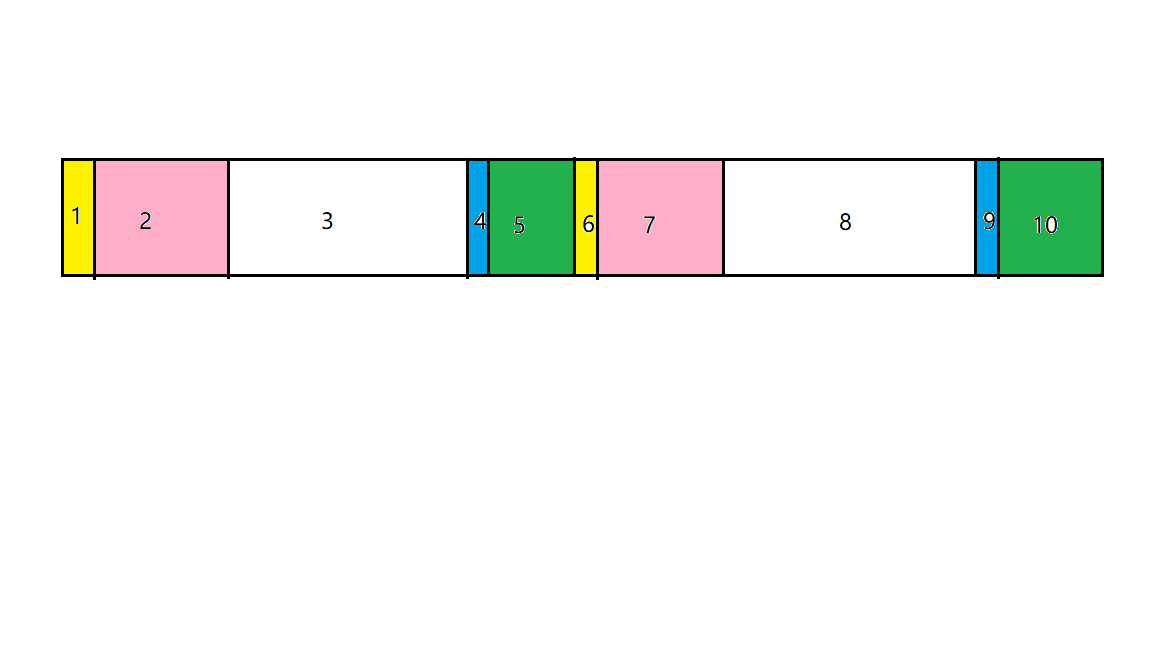
		左HEX	左Float	右HEX	右Float
1	负0	0x80000000	0	0x80000000	0
2	负非规格化数	0x80000001	-1.401298464e-45	0x807FFFFF	-1.175494211e-38
3	负规格化数	0x80800000	-1.175494351e-38	0xFF7FFFFF	-3.402823466e+38
4	负无穷	0xFF800000	-inf	0xFF800000	-inf
5	-NaN	0xFF800001	-NaN	0xFFFFFFFF	-NaN
6	正0	0x00000000	+0	0x00000000	+0
7	正非规格化数	0x00000001	1.401298464e-45	0x007FFFFF	1.175494211e-38
8	正规格化数	0x00800000	1.175494351e-38	0x7F7FFFFF	3.402823466e+38
9	正无穷	0x7F800000	+inf	0x7F800000	+inf
10	+NaN	0x7F800001	+NaN	0x7FFFFFFF	+NaN

那么就比较容易的看出来，只有当是负0、负非规格化数、负规格化数和负无穷时，才需要使符号位取反。我们可以利用带符号整型int来进行大小比较，发现需要反转符号位的，机器码以int解释时均小于等于0xFF800000，即-inf的最大值。可以利用这一特性进行处理。

float_f2i

Description

Return bit-level equivalent of expression (int) f for floating point argument f.

Legal ops

Any integer/unsigned operations incl. ||, &&. also if, while

Max ops

Code

int float_f2i(unsigned uf) {
    int re = 0;
    int sign = uf >> 31;
    int expo = (uf & ~(1 << 31)) >> 23;
    uf = uf & ~(1 << 31);
    if (uf == 0) return 0;
    if (expo >= 0 && expo < 255)
    {
        expo = expo - 127;
        if (expo < 0) return 0;
        if (expo >= 31) {re = 1 << 31; return re;}
        uf = ((uf >> (23 - expo)) & ~(0xFF << expo)) | (1 << expo);
        re = uf;
        if (sign) re = 0 - re;
        return re;
    }
    re = 1 << 31;
    return re;
}

Thought

首先把符号位、阶码分离出来，分别放到sign和expo中。通过上题的表可以知道，非规格化数整数部分一定为0。除了0和规格化数、非规格化数外，其他的都是越界的无法表示的数，统一输出0x80000000。对于0，直接特判一下即可。所以只剩下了规格化数和非规格化数。

当计算出的阶码-127，即真实的2的阶数时，可以知道，如果小于0，那么预留的1也会到小数点以后，所以一定输出0。当真实阶数大于等于31时，预留的1加上左移到小数点前的数共32位，而且第一位是1，所以越界成了负数，也输出0x80000000。其他情况就直接保留左移后的小数点前的部分，如果符号位为1取个负，输出即可。

float_half

Description

Return bit-level equivalent of expression 0.5*f for floating point argument f.

Legal ops

Any integer/unsigned operations incl. ||, &&. also if, while

Max ops

Code

unsigned float_half(unsigned uf) {
  unsigned re = 0;
  int add = 0;
  int sign = uf >> 31;
  int expo = (uf & (0x7FFFFFFF)) >> 23;
  int monti = uf & (0x007FFFFF);
  if (expo == 255) return uf;
  if (expo >= 126) {expo = expo - 1; re = (sign << 31) | (expo << 23) | monti;}
  else {
    if (((monti & 1) == 1) && (((monti & 2) >> 1) == 1)) add = 1;
    re = ((sign << 31) | (expo << 22) | (monti >> 1)) + add;
  }
  return re;
}

Thought

首先判断是不是NaN或者infinite，他们的共同点是阶码为255，特判一下就好。

然后找规律，发现阶码>=126的时候，乘0.5 <=> 除以2 <=> 阶码-1；

否则，阶码和尾码统一右移一位。但是注意，会有向偶数舍入。

正确性有待验证~反正AC了~

南京航空航天大学 计算机组成原理实验 Lab1 Data-Lab

bitXor

Discription

Legal ops

Max ops

Code

Thought

minusOne

Discription

Legal ops

Max ops

Code

Thought

leastBitPos

Description

Legal ops

Max ops

Code

Thought

allEvenBits

Description

Examples

Legal ops

Max ops

Code

Thought

byteSwap

Description

Examples

Legal ops

Max ops

Code

Thought

isAsciiDigit

Description

Examples

Legal ops

Max ops

Code

Thought

satMul2

Description

Examples

Legal ops

Max ops

Code

Thought

subOK

Description

Examples

Legal ops

Max ops

Code

Thought

isLess

Description

Examples

Legal ops

Max ops

Code

Thought

bitMask

Description

Examples

Legal ops

Max ops

Code

Thought

leftBitCount

Description

Examples

Legal ops

Max ops

Code

Thought

logicalNeg

Description

Examples

Legal ops

Max ops

南京航空航天大学计算机组成原理实验 Lab1 Data-Lab